Author: csadmin

Although this is a chapter on off-axis parabolas (OAPs), I want to start with one more way of testing symmetric parabolas because it illustrates a point about off-axis alignment. Assume we have a symmetric parabola with no central hole and we want to minimize the obstruction due to testing. If we set the parabola up in front of an interferometer with a reference transmission flat, then we can place a ball centered on the focus to give a double pass test as in Fig. 1.

Fig. 1 Symmetric parabola in front of an interferometer transmission flat

The blue curve is the parabola, and the red lines are rays normal to the reference flat (magenta) reflecting off the parabola to the green ball used as a convex spherical mirror. The shorter radius black circle matches the radius of curvature of the parabola at its vertex and shows that the parabola’s radius of curvature gets longer as you move to the edge of the parabola. This is why you need a null lens to test a parabola at its center of curvature.

The longer radius black circle has its center of curvature at the 7/10ths zone of the parabola, or where a normal from a zone 7/10ths (sqrt(2)/2 of the way to the edge) intersects the axis of the parabola. If you were not using a null lens, this is where you would focus to minimize the difference between the parabola and a spherical wavefront. All this may seem off the subject until we ask how we should align the parabola in front of the interferometer?

As in Chapter 17, we know that 3 degrees of freedom of alignment are satisfied when the light from the interferometer is centered on the ball. In terms of fringes, this means no tilt fringes, the exact equivalent of light returning centered of the crosshair of the PSM when it is the test device. The rest of the alignment for the remaining two degrees of freedom concerns the most efficient way to adjust the parabola to remove the aberration, coma in this case, of a symmetric parabola.

Fig. 2 shows the misaligned parabola with the light still centered on the ball. The Figure is far enough misaligned so some aspects are not exact, but exaggeration was necessary to show the point about which the parabola must be rotated to keep alignment with the ball, namely about the intersection of the normal to the edge of the parabola and its optical axis.

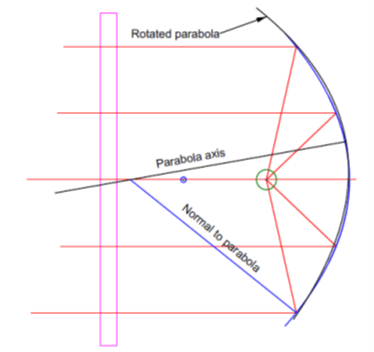
Fig. 2 Symmetric parabola aligned to a ball at its focus but rotated about the intersection of the normal to the edge of the parabola and its optical axis

The black line is the axis of the rotated parabola, and the blue line is the normal at the ray intersection close to the edge of the parabola. The small blue circle is the center of curvature of the vertex of the parabola at twice the focus distance. You can see the close to zero match at both edges and the center of the parabola and the “S” shaped, or coma, departure at roughly half the zonal radius of the parabola. Rotating about the intersection of the normal at the 7/ths zone and axis the parabola brings it into alignment with the flat to remove the comatic aberration while not shifting the focus off the center of the ball. The intersection is at the sagittal focus of the parabola for the zonal radius indicated by the blue line.

If you are testing a single parabola there is not much readily available hardware that lets you rotate about the sagittal focus, so you must iterate translation and tilt to achieve alignment. However, if you are doing production alignment, then it makes sense to custom design a fixture that lets you rotate about this point to achieve rapid alignment.

When we think about an off-axis parabola, the symmetry about the optical axis is broken, and the point about which we rotate for alignment is not the sagittal center of curvature, but the tangential center which lies on the normal but off the axis of the parent off axis parabola [1].

When we align an off-axis parabola the usual method is just as in the case of the symmetric one, use a focused beam at the focus of the OAP and have the light collimated by the OAP reflect off a plane mirror to the OAP and back to the focus. It looks so simple in a drawing like Fig. 3. In practice, it is maddeningly frustrating unless you have thought through the process thoroughly, and even then, it is hard. There are several things you can do to make it easier.

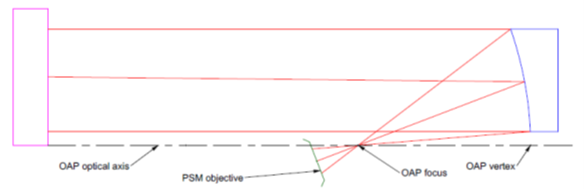
Fig. 3 OAP tested at its focus

Use a low power objective on the PSM at the OAP focus so you have a large field of view to capture the reflected light. Keep the plane mirror as close as possible to the OAP to minimize the length of the path back to the OAP and thus the decenter of the reflected path. (Once you are aligned, it is easy to move the plane mirror back away from the OAP to give you more room because the OAP and PSM establish the axis to the plane mirror.) Adjust the distance between the focused light source and the OAP to give approximately collimated light reflected from the OAP on the first reflection. Of course, use an aluminized plane mirror because you need all the light you can get to see the beam reflected from the plane mirror. Dimming the lights in the lab also helps.

Once the reflected light is approximately centered on the OAP you will see the focused spot in the vicinity of the focused spot exiting the objective. Continue to make small adjustments until light enters the objective. Now you can center the aberrated blob of light on the PSM crosshair to know that the light is normally incident on the plane mirror. Now make a small compensating tilt of the plane mirror and decenters of the PSM to keep the blob of light centered and well-focused while reducing the size of the aberrated image. It is easier to make the initial adjustments so the aberrated image is aligned to the axis of one of your adjustments and then shrink the image size by adjusting in the other axis. Continue until the spot is as small and round as possible.

The process of tilting the plane mirror and moving the PSM is effectively rotating the combination of mirror and OAP around the tangential radius of curvature of the OAP. If the OAP is mounted with 5 adjustments, it can be moved around the same point while the PSM and plane mirror stay fixed.

If there are space constraints, or other reasons, the OAP can be aligned by placing a ball at its focus and using the PSM as an autocollimator as in Fig. 4 that is an off-axis version of Fig. 1. During the initial setup adjust the PSM and OAP to get as round as possible light spot on a white card at the parabola focus before inserting the ball. Then adjust the ball in 3 DOF to get light back in the PSM. Continue adjusting the ball until the aberrated image is centered on the crosshair.

The order of making the initial adjustments may have to be changed if the center of the ball must be at a specific location relative to other features of the test setup. In some cases, not only will the ball location be fixed but the direction of the collimated beam is fixed so that all five degrees of freedom must be adjusted using the OAP.

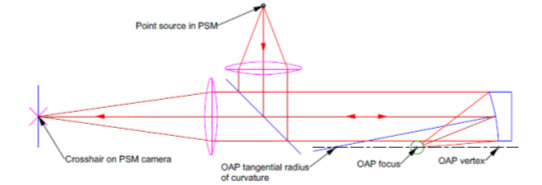
Fig. 4 PSM used as an autocollimator for OAP alignment

Notice there is a 6^th degree of freedom, but it has relatively loose tolerances in most cases. This degree of freedom keeps the beam centered on the clear aperture of the OAP to avoid vignetting. This is important but not to the 1 um and 1 arc second level necessary to eliminate aberrations.

With the spot centered on the crosshair of the PSM in autocollimator mode, it is easy to see whether the spot is in best-focus and whether it is aberrated because the illumination is a point source. The routine for final alignment is the same as before. Compensating tilt and decenter motions are made on the OAP to keep the spot centered and in focus while reducing the aberrations to get a small, round spot centered on the crosshair.

This method of using the PSM as an autocollimator to align the OAP may be more difficult to align initially but it may be the only option when there is a small space in a vacuum chamber or similar apparatus. The good news is that there is a way of performing precise alignment where it would be close to impossible any other way.

That is all for now, but we will have some future discussion about aligning conic optics using the focus and radius of curvature. This way you do not have to rely on aberrations but can set the axis of the OAP to a precise position.

[1] Smith, W. J., Modern Optical Engineering, 3^rd. Ed., p. 485, McGraw-Hill, NY, (2000).

I often receive requests for assistance with aligning parabolic mirrors, particularly off-axis ones. Interestingly, with the right tools, the actual alignment process is often quicker than mounting the optical alignment equipment. This observation led me to reflect on the tools themselves. Currently, no traditional method—whether using an autocollimator or an alignment telescope—provides an effective way to align a parabola with a plane mirror.

In this chapter, I will explore the practical alignment of parabolic mirrors, beginning with full, rotationally symmetric mirrors and progressing to off-axis mirrors in the following chapter. The focus will be on practical approaches and techniques, rather than the theoretical concepts typically found in textbooks.

A parabolic mirror perfectly images collimated light to a focus if the optical axis of the parabola is perfectly coaxial with the incident light. In practice, what is wrong with this statement? The instrument at the focus obscures some to all the incident light, depending on the size of the mirror. It is easy to draw Fig. 1a in a textbook, but it does not show the actual situation in Fig. 1b, let alone Fig. 1c, with a small mirror.

Fig. 1 a, light from infinity coming to a focus. Fig. 1 b, light is partially blocked by the test instrument; Fig. 1 c, light is blocked by the test instrument, as might be the case for a small mirror.

For the same practical reasons, we assume that a symmetrical parabola—such as the one used in a Newtonian telescope with a diagonal plane mirror to bring the focus outside the telescope—results in some degree of obscuration. The difference between the practical use in the telescope and testing the uncoated parabola right off the polishing machine is that the test instrument is larger than the diagonal mirror unless the parabola is larger than the ones in most amateur telescopes.

Fig. 2 Symmetric parabola focused as in a Newtonian telescope to show that the obscuration of the diagonal may be less than that due to the test instrument (blue rectangle)

It is clear from Fig. 2 that we can reduce the obscuration due to the diagonal for test purposes by moving it farther from the parabola so the test obscures less of the aperture than when used as a telescope.

Another practical test problem is how to simulate light from infinity. Once the aperture of the parabola is larger than about 100 mm, the cost of the collimator used for testing is more than the cost of making the parabola. This expense is why we test most parabolas in double pass off a plane mirror, a less costly test arrangement for a large symmetric parabola. As parabolas get larger, they usually have a hole around the vertex since this mirror part is obscured. The hole opens many test options, as in Fig. 3, where there is no longer an obscuration due to the test instrument. Another advantage is that the test instrument has a light source producing heat. When the instrument moves outside the test path, the heat-produced turbulence problem goes away.

Fig. 3 Parabola with a central hole tested against a plane mirror

The plane mirror must be high quality as the light path hits it three times. The mirror must also be highly reflective since the parabola under test will usually be bare glass. The light is incident on it twice, so only 0.16% of the initial light is reflected into the test instrument. If the test instrument is an interferometer, a standard transmission sphere designed for use with bare glass will not produce high-contrast interference fringes. On the other hand, if the test instrument is an autostigmatic microscope such as a PSM, there is plenty of light to align and analyze the image.

Fig. 3 shows the test in perfect alignment, but that is not the situation when we first set the plane mirror and parabola on an optical table for testing. The situation will be like that shown in Fig. 4, where the point source of light at the PSM focus reflects back displaced and out of focus.

Fig. 4 Same as Fig. 3 except slightly misaligned by tipping the plane mirror and shifting in axially

Fig. 4 assumes the plane mirror was rotated 0.4 ° about its vertex and shifted axially toward the microscope objective of the PSM. The reimaged focus is shifted laterally and axially due to the misalignment. In addition, the nominally parallel rays from the parabola are no longer normally incident on the plane mirror. This detail illustrates the first step in aligning a parabola; we move the PSM until the reimaged focus lies on the crosshair of the PSM and is in focus. When this condition is met, the collimated light from the parabola is normally incident on the plane mirror. This first step of the alignment only locks down 3 degrees of freedom because all we see is a single point at the reimaged focus. The remaining 2 degrees of freedom account for the aberrations in the reflected image.

It is clear from Fig. 4 that if we move the PSM objective upward about half the lateral separation of the foci and to the right slightly, the reimaged focus coincides with the focus of the light launched from the PSM. However, since we did not move the parabola, its axis remains 0.4 ° non-normal to the plane mirror and causes aberrations in the image. If we rotate the flat to remove the aberrations, the reimaged focus will move off the PSM crosshair. To reach complete alignment with no aberrations, we move the PSM laterally as we rotate the plane mirror to keep the reimaged focus centered on the crosshair. It is evident when you adjust in the right direction because the aberration, coma for a symmetric parabola, will decrease as we gradually move the mirror and PSM to keep the image centered. A simple way to see why you get aberrations even though the rays are incident on the plane mirror at normal incidence is to consider Fig. 5a, where rays from infinity are incident on the parabola so that the rays and parabola optical axis are parallel. Fig. 5b shows the parabola rotated about its vertex by 1°. This rotation moves the focus below the ray incident on the mirror’s center. It appears this is all that has happened until you look closely, as in the detail around the focus in Fig. 5c, where the ray from the center in the parabola is 13 µm above where the marginal rays focus, producing an aberrated image.

Fig. 5 An aligned parabola, left, parabola rotated 1° to incident rays, middle, and a 70x detail of the immediate region around the focus showing the spread in rays due to the misalignment.

Here is a good place to recap what we discussed about aligning a symmetric parabola to a plane mirror where we assume we have a central hole in the mirror. Using the setup in Fig. 3, we can precisely locate the parabola in 3 degrees of freedom by assuring the return reflection is in focus and centered on the PSM crosshair. We remove the remaining 2 degrees of freedom using aberrations. When I say the return image is centered on the PSM crosshair, I am saying that the centroid of the aberrated image is centered on the crosshair. This determination gets more precise as we adjust the setup to remove the aberrations, consequently making the image smaller and rounder.

We are constrained to using aberrations for the remaining two degrees of freedom because we do not have information about the plane mirror relative to the PSM. However, we can measure the tilt of the PSM to the mirror by using it as an autocollimator by removing the objective, as shown schematically in Fig. 6.

Fig. 6 Aligning parabola in all 5 degrees of freedom with a PSM by using it as both an autostigmatic microscope with an objective and as an autocollimator without the objective

All five degrees of freedom are accounted for since we define a line or an axis by a point and two angles. The only position where the parabola can be located—while still reimaging the point of light at the PSM objective focus and ensuring it is centered on the PSM crosshair—is when the parabola’s axis is perpendicular to the plane mirror. Practical considerations also come into play: the PSM must be securely mounted to prevent movement when the objective is removed, there must be sufficient space behind the parabola to facilitate objective removal, and the objective must consistently screw into its holder without causing lateral shifts. Typically, lateral shifts are less than 5 µm, meaning that if the parabola’s focal length exceeds 500 mm, the resulting error from such shifts is less than 1 second of arc. Now that we have covered the alignment of symmetric parabolas both by using aberrations and 5 degrees of freedom, we will cover off-axis parabolas in Chapter 18. In some ways, they are easier to align than symmetric ones because you don’t have to worry about obstructing the beam.