Lens Centering Using The Point Source Microscope

ABSTRACT

Precision lens centering is necessary to obtain the maximum performance from a centered lens system. A technique to achieve precision centering is presented that incorporates the simultaneous viewing through the upper lens surface of the centers of curvature of each element as it is assembled in a lens barrel. This permits the alignment of the optical axis of each element on the axis of a precision rotary table which is taken as the axis of the assembly.

1. INTRODUCTION

Lens centering is a crucial step in the manufacture of rotationally symmetric optical systems. For optical systems to deliver maximum performance the optical design must be superior, the lens elements accurately manufactured and the elements well centered in a barrel. With experienced designers, sophisticated software and vast computing power, superior designs are easier to produce than in the not too distant past. With phase shifting interferometers and mature computer controlled polishing it is possible to produce optical surfaces accurate to a few nm rms or better.

In order to take full advantage of an excellent optical design and well manufactured optical surfaces the lens elements must be well centered in the assembly. Without a careful and accurate job of centering the money put into design and polishing will be lost. This paper discusses how to do a superior job of lens centering by simultaneously sensing both centers of curvature of each element from above as the element is placed in the lens barrel and the barrel is rotated about its axis. Each element is adjusted in tilt and decenter until there is no motion in either center of curvature.

To demonstrate this procedure we will first discuss the definition of centering and give a specific lens design as an example. Then we will show how to locate the centers of curvature of the lens surfaces looking from one side of the lens only. The instrument used to optically locate the centers of curvature, an autostigmatic microscope that we have called the Point Source Microscope (PSM), will be described and an example of how it would be used to find the center of curvature for each lens surface will be given.

Finally we discuss how the tilt and decenter of the surfaces affect performance of the lens system and how sensitive the PSM is to these centering errors to give a feel of the performance improvement using this superior centering technique. This leads directly into the conclusions.

2. DEFINITION OF CENTERING

2.1 Optical axis of a lens element

The optical axis of a lens is the line between the centers of curvature of the two surfaces. It is a paraxial property that is seldom given any thought but is the basis for this discussion. Aspheric surfaces do not change the definition. If the whole aspheric surface produces too much spherical aberration to center on the reflected return image the surface may be stopped down to effectively make the surface paraxial.

There are several things to note about this definition; it is completely independent of the mechanical features of the lens such as the periphery or seat, and the definition is incomplete without considering both lens surfaces because a single sphere has no intrinsic axis. If a lens is poorly centered its periphery is not concentric with the optical axis nor is its seat perpendicular to the axis, but it still has a well defined optical axis.

In terms of the larger aspects of a lens system, if both object and image lie on the optical axis of the lens system it is being used on-axis. If one or more elements within the lens system are decentered it becomes difficult to define the axis of the system. Probably the best definition then is the angle the lens must be tilted to produce the best image, that is, how must the lens be tilted about the line joining object and image to produce the best image.

2.2 An example lens system

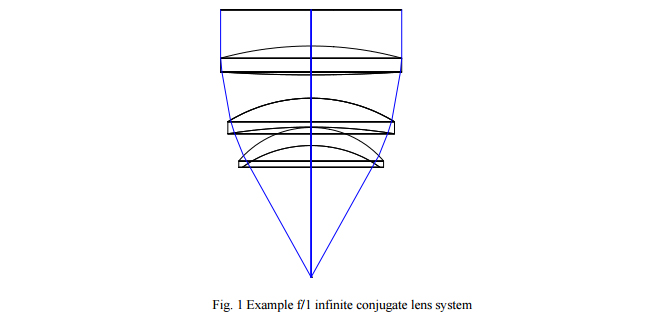
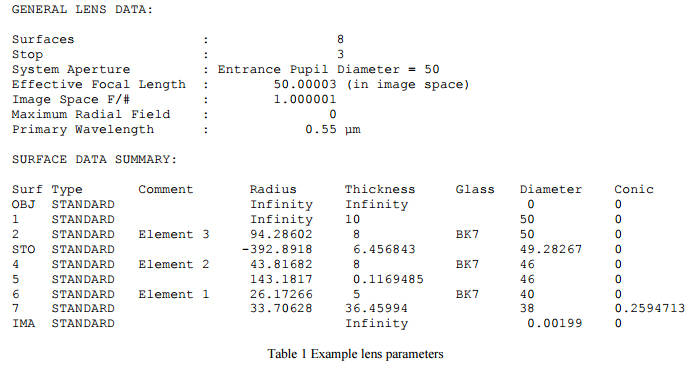
To demonstrate the ideas about centering we give the design of a three element, all BK7, f/1 infinite conjugate lens with one aspheric surface. The design is shown in Fig. 1 and the parameters given in Table 1. The design has about 0.035 waves P-V of spherical aberration and is 0.0075 waves rms at the design wavelength of 0.55 µm.

3. LOCATING THE CENTERS OF CURVATURE OF THE LENS SURFACES

Before looking at the centers of curvature of the lenses we show the three lens elements in their cell (see Fig. 2) to give a feel for the physical constraints on centering. The cell is sitting on top of an air bearing rotary table and has been adjusted so there is zero runout or decenter and no tilt, that is, the axis of the cell is coincident with the axis of the rotary table. It is further assumed there is no error in the table bearing, an assumption good these days to 50 nm sorts of dimensions.

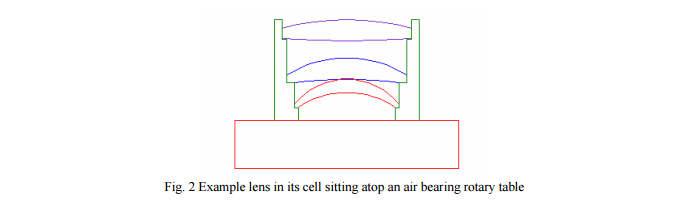
It is clear from Fig. 2 that all optical sensing of the centers of curvature of the elements must be done from above the lens system. While rotary tables are available with through holes1 and use of the underside of the lens may make some examples easier, particularly in volume production, we show there is no need to view the lens from the bottom.

It is clear how to locate the centers of curvature of the upper sides of the lenses, the centers of curvature lie a distance equal to the radius of the upper surface below the lens element in question. A positive lens with a long working distance, or back focal length, will have to be placed above the example lens system. As a reasonable choice a 100 mm efl lens could be used because the longest convex radius is 94.286 mm on the upper surface of Element 3.

Now we will use this positive lens along with a lens design program such as Zemax2 to find the apparent location of the center of curvature of the rear surface of each lens element looking through the upper surface. For Element 1, the first one that will have to be inserted in the cell, the Lens Data Editor is set up as in Fig. 3.

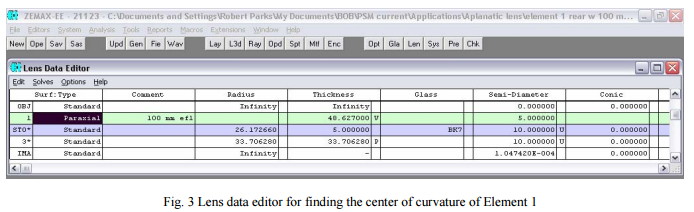
The object is set at infinity feeding the paraxial (perfect) 100 mm efl lens that is surface 1. The distance (thickness) between the paraxial lens and the front surface (line 2) of Element 1 is the unknown (or variable) we must find. On that line (2, also the stop in the system) is the radius of the upper surface, 26.172 mm, the thickness of the lens, 5 mm, and the material, BK7. The next line (3) is the rear surface of Element 1 with a radius of 33.70628 mm. If the light is to strike that surface at normal incidence, the condition necessary when a point source is at the center of curvature, the light must come to focus a distance equal to the radius of the surface farther to the right. That is why the thickness for the rear surface is also 33.70628 mm as is assured by using a pickup (P) from the radius column.

The next, or image, line shows the light is focused at this distance because the diameter of the image is very small when the thickness from the paraxial lens to the front surface is 48.627 mm, a value found by using the design optimizer.

Notice the thicknesses do not add to 100 mm showing the effect of refraction at the front surface. Another way of finding the distance between the center of curvature and the front surface of the lens is to use paraxial ray tracing to find that

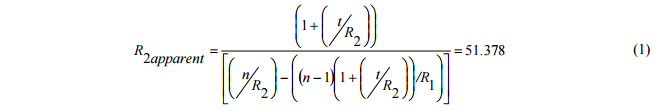
Notice this is just the paraxial lens focal length minus the paraxial lens to front surface thickness of 48.627, or 51.373. The 5 µm difference between the results can be accounted for by not using a small enough aperture size to make the lens design optimizer give a truly paraxial result.

Fig. 4 shows the results of using this same technique on all three lens elements in the system. Notice for Element 1 that the distance from the rear surface to the focus, 46.373, plus the lens thickness, 5, and the distance from the lens front surface to the paraxial lens, 48.627, add to 100 mm, the efl of the paraxial lens. Also shown are the physical centers of curvature of the two surfaces. The same logic holds for the other two elements but in these cases the center of curvatures of the rear surfaces after refraction are above the front surface by 556.182 and 106.416 mm for Elements 2 and 3, respectively.

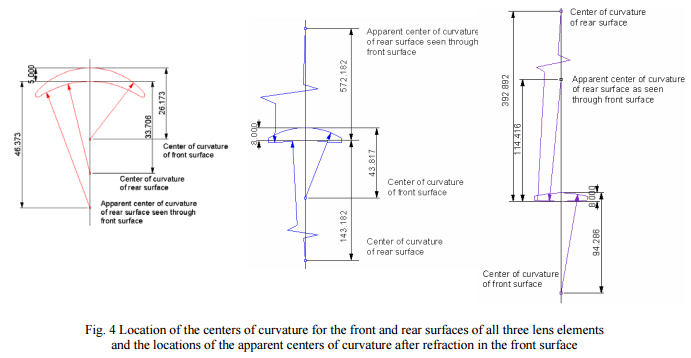
Although the example lens system does not have a concave front surface it is obvious that the center of curvature of this surface would be above the surface by the radius of the front surface. The method for finding the location of the center of curvature of the rear surface after refraction in the front is the same as for this example. Now that we have shown how to locate the centers of curvature of both lens surfaces from above the lenses we show how to use the Point Source Microscope (PSM) to view these locations.

4. POINT SOURCE MICROSCOPE (PSM)

The PSM is a video metallographic, or reflected light, microscope using Köhler illumination to provide uniform intensity over the field of view. In addition, the PSM has a point source of illumination produced by the end of a single mode fiber pigtailed to a laser diode that is conjugate to the microscope object plane as shown in Fig. 5 below. This point source of light makes the PSM into an autostigmatic microscope, and it is this feature that is used to view the centers of curvature of lens elements during centering.

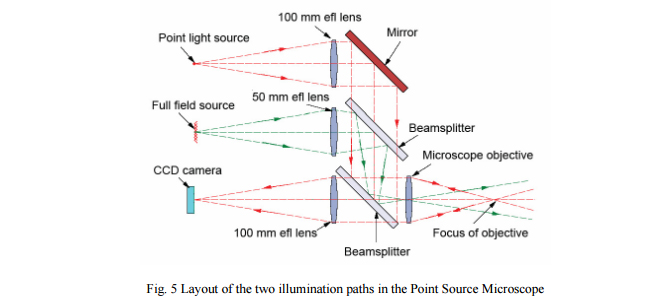
When the point light source is used and the focus of the microscope objective is conjugate with the center of curvature of a lens element or mirror surface the light will strike the surface at normal incidence and be reflected back to the microscope objective focus and on to the CCD detector where it can be viewed on a monitor. When the alignment with the center of curvature is precise in lateral position and focus the return spot will be a well focused and centered on the detector. If the alignment and focus are less than ideal the spot will be defocused and decentered as shown in Fig. 6.

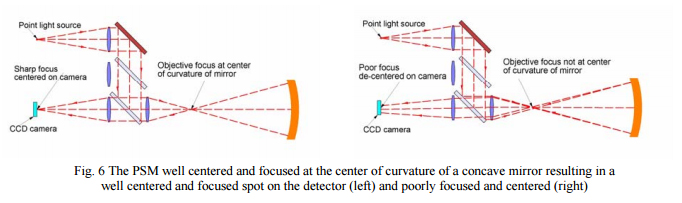
It remains to show how two PSMs can be set up to view both sides of a lens element simultaneously so the optical axis can be established and aligned. It is also obvious that there are limits as to how well lenses need to be centered and the PSM can be used to tell if the centering is good enough by measuring the excursion of the return spot of light as the rotary table is turned.

5. VIEWING BOTH CENTERS OF CURVATURE SIMULTANEOUSLY

5.1 Scheme for simultaneous viewing

Because the optical axis of a lens element is the line joining the centers of curvature and it is that axis that must be aligned to both the cell axis and the other elements within the lens system it is most expedient to view both centers of curvature simultaneously during centering. Although the centering operation can be done be viewing just one center at a time it is very tedious to do it this way because the alignment of one center may, and usually does, disturb the centering of the other.

Going back to our example lens we look at Element 1 first. In Fig. 7 we show just the location of the upper or front surface center of curvature and the rear surface center after refraction in the front surface because these are the two centers we see with an autostigmatic microscope

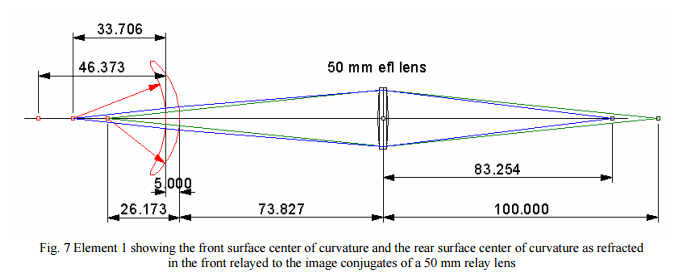
Now instead of using a 100 mm efl lens at infinite conjugates we use a 50 mm efl lens at 1:1 finite conjugates to relay the front surface center of curvature to the right side of the 50 mm lens. However, this same lens can be used to relay the rear surface apparent center of curvature with an object conjugate of 125.20 mm to the right side with an image conjugate of 83.254 mm accomplishing just what we wanted to do, image both centers of curvature simultaneously. It now remains to separate the centers so they can each be viewed without having to move a PSM.

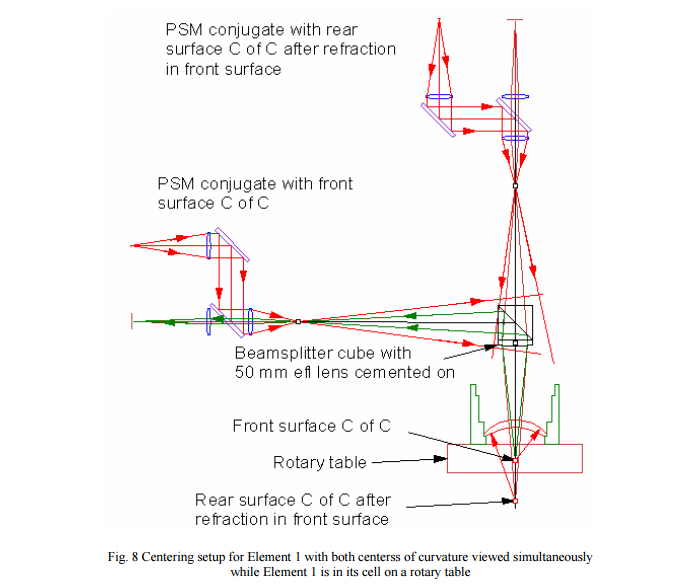
This is most easily accomplished with a minor modification to the layout in Fig. 7, the introduction of a beamsplitter with a 50 mm efl lens cemented to it so there is only one optical component above the lens element being centered. The setup will then look like that in Fig. 8 where the optical paths of both PSM’s are shown. We have neglected the slight axial shift in the conjugates due to the optical thickness of the beamsplitter as well as the small introduction of spherical aberration it will produce. In practice the f/number of the cone of light used for centering is so narrow that the exact axial position and small amount of aberration is not critical. Further, all the conjugate calculations have been first order, or paraxial, so they are not exact but close and quite good enough for real implementation because what we are ultimately interested in is whether the relayed return spots from the centers of curvature move or not as the rotary table is turned.

5.2 Modification for viewing with two autostigmatic microscopes

Fig. 8 is rather busy but it shows the entire setup for centering Element 1. The two PSM’s send out cones of light that somewhat over fill the beamsplitter/relay lens combination and the relay lens serves as the stop as it sends converging beams of light to both the center of curvature of the front surface and to the center of curvature of the rear surface after the light has been refracted in the front surface. The light reflects off the front and rear surfaces of the lens and retraces itself back into the two microscope objectives. Both reflected light beams enter both objectives but the beams from the incorrect conjugates are so far out of focus that very little light reaches the detector and is inconsequential. Only light from the correct conjugate is well focused and bright on the detector of that PSM.

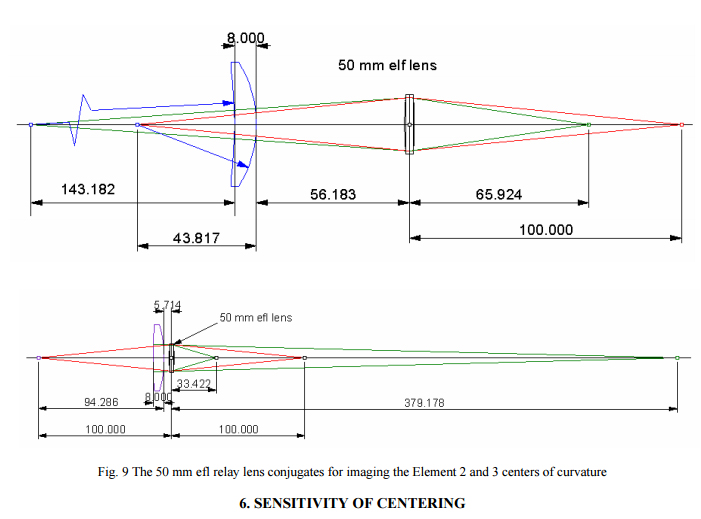
Similar setups work for the other two lens elements even though the rear surface centers of curvature appear above the front surface. Fig. 9 shows the conjugates for these two elements using the same 50 mm efl finite conjugate lens. In this example it just turned out that the same focal length lens could be used for all three elements. In general this will not be the case but a relatively few beamsplitter/relay lens combinations can be used for practically any lens element that needs centering. In fact, the relay lens is only 5.714 mm in from of Element 3 in Fig. 9, a distance that may be too close for comfort. A 60 or 75 mm efl relay lens could have been used just as well without much increase in the total dimensions of the measurement setup. Obviously all the relay lens conjugates would differ from the example.

It is further clear that the relay does not have to be used at 1:1 conjugates in one of the cases. The options for finding suitable conjugates is almost limitless, something that is a possible drawback in finding good conjugate solutions. However, it does show the flexibility in this system of simultaneous conjugate viewing. Along the same line the PSM does not have to be used with expensive microscope objectives since this application does not call for full field imaging. Inexpensive, longer focal length doublets can be mounted in lens tubes and mounted to the PSM using objective adapters. The beamsplitter would still have to be used but all the optical power would be in the PSM itself.

6. SENSITIVITY OF CENTERING

6.1 Theoretical considerations

Now that we have seen how to view both centers of curvature simultaneously we need to ask how sensitive are the PSM’s to tilts and decenters of the three lens elements in this example. For the front surfaces this is easy; if the surface is decentered 1 µm, the return spot will move by twice that because of the doubling on reflection. When the lens is rotated 180º with the rotary table the lens is decentered in the opposite direction so the total spot motion is 4 µm for a 1 µm decenter from the rotary table axis of rotation. Depending on the objective used, and the 5x would be typical for centering operations, there is another factor of 2.5 so the image motion at the detector is 10 µm. The detector has 4.65 µm pixels and can centroid to 0.1 pixels. Working backwards gives us a theoretical sensitivity to front surface decenter of about 47 nm.

Regarding rear surface decenters, clearly a front surface decenter will affect the apparent decenter of the rear surface. Rather than do a lot of calculations the pragmatic approach is to center the front surface first and then the rear surface decentered will not be affected except by a scale factor.

For tilts the sensitivity is linearly proportional the radius of curvature (or apparent radius) of the surface in question. Working backwards from the above example we find the sensitivity to tilt about 10 seconds of arc per mm of radius. Thus if a concave surface had a radius of 10 mm the PSM would be sensitive to a 1 second tilt of the surface and to a 0.1 second tilt if the radius of the surface were 100 mm.

It may be asked what is the effect of a tilt or decenter on the lens performance. A tilt displaces the chief ray so the lenses following the tilted element are in effect decentered. A decentered lens deviates the chief ray from the optical axis making the lenses following appear to be tilted. This is nicely shown in a recent paper by Burge³.

6.1 Practical considerations

Now it is time to look at the real situation in most instances in terms of lens edging and assembly in a cell. We will first look at assembly to gain an insight as to what we need to look at in terms of edging tolerances. When a lens is set in a cell the lower spherical surface seats on a step shaped land that was machined into the cell that is concentric with the axis of the cell in the radial direction and perpendicular to the axis in the axial direction as shown in Fig. 10. In a perfect world where there are no burrs or contamination on the seat this arrangement assures that the center of curvature of the lower surface lies on the axis of the cell.

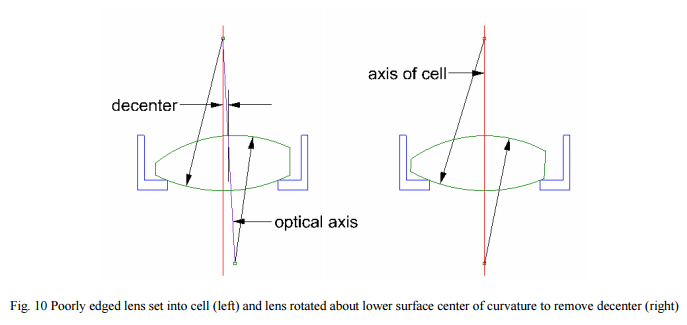
The upper surface center of curvature will not lie on the axis of the cell if the lens was poorly edged, and in general, will not lie on the axis anyway. The optical axis of the lens is shown on the left of Fig. 10 and shows the decenter of the upper surface. This is easily corrected by decentering the lens to bring the upper surface center of curvature onto the axis of the cell. The lower surface remains centered because the edge of the seat is equidistant from the center of curvature of the lower surface. Clearly the cell bore must be sufficiently oversize to permit the decentering of the lens.

This brings us to tolerancing for edging in the case where lenses will be centered in a cell during assembly. Many lens design programs have automatic tolerancing schemes built in and they vary every possible lens parameter to see the effect on performance. Single surface tilts help with tolerancing the seats in the cell but have nothing to do with the lens element as a whole. Further, since the rear surface of the lens always (in a perfect world) stays aligned the tilt and decenter of the upper surface are one and the same; removing the decenter removes the tilt and vice versa. This means the lens element does not have to be toleranced for both.

Ultimately the consideration will come down to how much oversize does the bore have to be to insert the element without it getting hung up in the bore and how much clearance must be allowed for thermal changes between glass and cell, and what is the minimum practical thickness for a shim to center the lens in the cell. The answer to shim thickness is about 10 µm and numbers comparable to this for the other considerations for lenses in the 25 to 50 mm diameter range. It is such considerations that help with the decision to tolerances and not try to center during assembly or looser edging tolerances and center during assembly. This also becomes a question of how many units will be produced and the diameter of the elements. Clearly the shorter the focal lengths and smaller the lens diameters the more critical the decentering in order to keep the ratio of decenter to focal length a small number.

For those who like to go through the tolerancing numbers without the obscuration of the software the reader is referred to an excellent book by Gerrard and Burch4 on matrix methods in optics.

7. CONCLUSIONS

With modern lens design, interferometric testing of optical surfaces and computer controlled polishing it is possible to produce suburb optical elements. All the potential gain in performance due to these factors can be lost at the last step of assembly unless there is a method of assuring the lens elements are well centered in their lens cell.

We have showed how to implement such a method to assure the centering as lenses are assembled using a precise rotary table and a modern version of the classical autostigmatic microscope. The method can sense the centers of curvature of both surfaces of an element so that any errors in tilt and decenter can be corrected during assembly to the sub-micron and sub-second level.

The device that makes this possible is a classical alignment instrument, the autostigmatic microscope fitted with a bright point source of light, a sensitive digital video camera and monitor to allow convenient viewing of the return image and software to process the video image to give metrics of the degree of centering.

In addition to its application in lens centering the Point Source Microscope is being used for the alignment of cell phone lenses, astronomical telescopes, and terahertz optics. Metrics are returned at frame rates so the effects of adjusting alignment can be viewed in real time. In some instances users are finding the PSM is more convenient and easier to use than more expensive interferometric test methods.

REFERENCES

1. J. Heinisch, et. al., “Novel Technique for Measurement of Centration Errors of Complex, Completely Mounted Multi- Element Objective Lenses”, Proc. SPIE, 6288, 628810, (2006). 

2. Zemax Development Corp., www.zemax.com.

3. J. Burge, “An easy way to relate optical element motion to system pointing stability”, Proc. SPIE, 6288, 628801, (2006). 

4. A. Gerrard and J. M. Burch, Introduction to Matrix Methods in Optics, particularly Appendix B, Dover Publications (1994).