Centering Steep Aspheric Surfaces

1. INTRODUCTION

Finding the optical axis of an aspheric surface is an essential part of making an aspheric lens because the center of curvature, or optical axis, of the second side must lie on, or be coincident with, respectively, the optical axis of the first side for maximum optical performance. Looking at the center of an aspheric surface and measuring the tilt and coma as a function of decenter is an obvious means of determining centration, but many aspheric surfaces are relatively spherical over the part of the lens aperture that can be viewed with commercially available optics and there is too little coma to make a useful measurement of decenter.

We describe an alternative method of viewing a small patch of the aspheric surface near the edge of the clear aperture where the asphericity is greatest while rotating the lens about an axis close to coincident with the optical axis of the surface. By also tracking the reflected light image when using an autostigmatic microscope (ASM), or using an interferometer to measure the low order Zernike coefficients, as the lens is rotated, both the tilt and decenter of the surface can be determined.

The relationship between the image motion and Zernike coefficients is described for both tilt and decenter of the surface as well as the means of separating the relative amounts of tilt and decenter are given. These methods of determining tilt and decenter seem to work for all aspheric surfaces we have tried to date.

We begin by reviewing the thinking that led to the method described for finding the optical axis of an aspheric surface. The discussion moves through successive attempts to find a method of locating the optical axis for aspheric surfaces that works for all surfaces that have enough asphericity to qualify as aspheres. Results are shown for both the interferometer and the autostigmatic microscope method*. Finally, we conclude by describing a method that may work even better for many aspheric lenses that makes use of a computer generated hologram.

*After submitting the Abstract for this talk it came to the author’s attention that there is a European Patent #EP 1918 787 A1 covering the autostigmatic microscope method described in this paper for locating the optical axis of the first surface of an aspheric lens.

2. BACKGROUND

In the process of manufacturing precision aspheric lenses and surfaces, particularly lenses molded of glass, plastic or other optically useful materials, it is imperative to know if the optical axes of the surfaces are coincident for the best optical performance of the lens. There must be neither tilt or decenter between the optical axes. This requires a method of measuring the axes of both aspheric surfaces relative to each other, or relative to a common reference.

One method in wide use is a Panasonic UA3P coordinate measuring machine that measures relative to a common reference by mounting the lens in a plate with a hole the diameter of the lens so the lens surfaces can be reached from either side of the plate. The plate also has 3 balls mounted so they protrude from either side of the plate. The plate mounts against “V” grooves so that the plate may be turned over without the axis of the plate being lost. This is how both sides of a lens are measured relative to a common axis.

Although the UA3P is widely used it has limitations; it measures by contacting the sample with a probe tip which may damage soft lens materials such as plastics. Even for small lenses the measurement time is long, and while very precise, the machine is very expensive.

Another way of measuring the optical axes relative to each other is to mount the lens centered on a post that is centered on a rotary table. As long as one can access the edges of the optical surfaces they can be measured relative to the common axis of the rotary table¹. Again it is a contact method and is not very useful for small lenses such as might be used in cell phones and endoscopes. Further, it cannot fully determine the difference between tilt and decenter of the optical axis because while this method measures out at the edge of an aspheric surface where it is most sensitive to measure for tilt and decenter of the axis, measuring only displacement and not simultaneously tilt leaves some ambiguity in the definition of the axis of the surface.

A further method is disclosed in US Patent Application 2010/0309458, “Asphere Measurement Method and Apparatus”, where two interferometers are used facing each other with the lens being measured in between the two. This method is non-contact and purports to determine the optical axes of the two surfaces by measurement of the profiles of the two surfaces. In practice this method works well for some lens designs but probes the lenses in the centers of their surfaces, the place on the surface of some lenses least sensitive to the determination of the optical axis. The method of aligning the two interferometers to each other is vague in the patent application, yet this alignment is vitally important for a precise measurement. Finally the method requires two complete interferometers.

3. METHOD USING THE CENTER AND EDGE OF THE SURFACE

3.1 Using an interferometer

One method of looking at both the center and edge of an asphere is to use two interferometers equipped with Mirau objectives that compare the aspheric surface to a plane reference. This is a practical method of looking at the surfaces because the Mirau objective is the interferometer, and thus the entire interferometer package can be kept quite small. This makes it convenient to mount an interferometer so that it can look at a portion of a surface near the edge of the aperture as shown in Fig. 1 where the whole interferometer package is a Point Source Microscope² (PSM) and PZT phase shifter to move the Mirau objective.

Fig. 1 A PSM based Mirau interferometer viewing near the edge of an aspheric lens sitting on a rotary table

As seen on the monitor the fringes from the interferometer show astigmatism that is not centered in the field of view. The low order Zernike coefficients in each interferogram will change as the lens is rotated on the rotary table unless the lens is well centered. By using Zernike coefficients from an interferometer and those from viewing at the edge of the aperture the tilt and decenter of the surface can be separated and measured. While this method works well, and provides high precision it is instructive to look at using an ASM to do the same measurement because the ASM is a less expensive solution and easier to implement. The ASM explanation also gives some insight into what the interferograms and Zernike coefficients show about the centering. Further, the ASM method has some advantages when trying to center the second surface of the asphere over the interferometric approach.

3.2 Using an autostigmatic microscope

Using an ASM to determine the optical axis of an aspheric surface goes back to fundamentals. An axis is a line and a line is determined by 2 points on the line, or a point and an angle. The line in this case is the line between the paraxial center of curvature (CoC) of the surface and the sagittal focus, the point defined by the normal to the surface at the edge of the clear aperture of the lens. To illustrate the concept and keep the math relatively simple a parabolic surface will be used as the example.

3.2.1 Centering geometry illustrated using a convex parabola

Consider a parabola with a 10 mm vertex radius large enough in diameter so that we can look at an annulus where the slope of the surface is 45°. Such a parabola is shown in Fig. 2 with relevant dimensions.

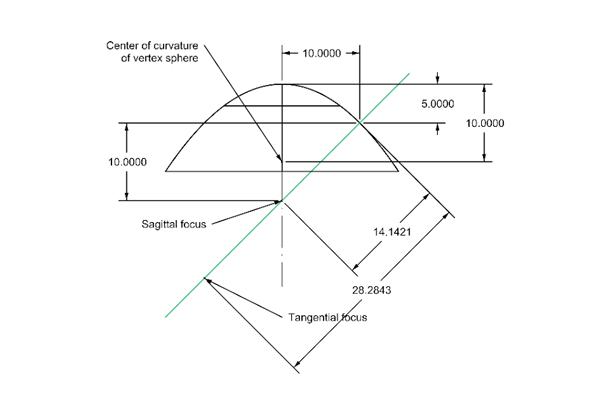
Fig. 2 Convex parabola with 10 mm vertex radius and zone at 10 mm radius

Before getting into the details of the dimensions in Fig. 2, it is important to understand the fundamentals of the problem of locating the optical axis of the aspheric surface. With an autostigmatic microscope (ASM) looking down in z along the optical axis and focused on the vertex radius of curvature, the position of the vertex CoC is monitored as the surface is rotated in azimuth about the z axis. The vertex CoC is one point on the optical axis and it is easy to get data in x and y on the ASM monitor as the surface rotates in azimuth, θ.

By looking normal to the surface toward the optical axis along a line 45° from the optical axis, the other point seen with an ASM is the sagittal focus, a second point on the optical axis. Since the sagittal focus is a line image in the plane of Fig. 2, it is ambiguous to measure the position of the line in a direction along the line image. However, it is easy to measure the displacement of the line perpendicular to the line. Fig. 3 shows a typical line image from the sagittal focus and it is clear that it is easy to determine the position of the line left to right, or in the x direction perpendicular to the line.

At first it seems the x location is insufficient information to determine the y position, but since the surface is rotating in θ, the y position of the line image will be 90° out of phase with the x position. This being the case, the two points on the line a known distance apart are completely defined, sufficient information to explicitly determine the optical axis of the surface relative to the axis of rotation of the rotary table.

Fig. 3 Image of the sagittal focus of an Edmund Optics asphere 69-141

This information also gives a means of calculating the sensitivity of the measurement based on the distance between the CoC of the vertex sphere and the sagittal focus. Clearly the angle of incidence of the beam focused at the sagittal focus should be chosen to maximize the distance between the CoC and the sagittal focus, usually a point at the edge of the clear aperture.

Another aspect of this geometry is that if the surface is moved relative to the axis of rotation so that there is no motion of the CoC, the surface is perfectly centered, that is, there is no decenter. If there is still motion of the sagittal image it is entirely due to tilt. This makes it easy to separate decenter of the surface from tilt, and makes the adjustment to eliminate tilt and decenter quite easy.

This geometry also sets up the possibility of measuring the relative tilt and decenter of the second surface of a lens by looking through the first surface. If there is no tilt or decenter of the first surface, there will be no motion of the reflected spots from the second surface introduced by the first. There will clearly be dependencies on the setup of the ASMs to measure the second surface that depend on the first, but once the first surface is centered and the initial setup is done, the first surface will not influence the second surface measurements as a function of θ.

3.2.2 Calculation of the dimensions of the relevant features of the parabola

Referring back to Fig. 2, the zone where the slope is 45° is 10 mm from the optical axis because y/R = 10/10 = 1 = tan(45°). The sag at y = 10 is y²/2R = 5 mm. The center of curvature of the vertex sphere is 10 mm below the vertex and the sagittal focus is sag + vertex radius = 5 + 10 = 15 mm below the vertex where the normal to the surface intersects the optical axis. The distance from the surface to the optical axis is sqrt(y² + R_v²) = sqrt(20) = 14.1421 mm, the sagittal radius, R_s. The distance from the surface to the tangential focus is R_t= R_s³/R_v² = 28.2843 mm, in this particular case of a parabola, 2*R_s.

If a converging beam of light from the ASM is directed normal to the surface at the zone y = 10 and is focused at the sagittal focus, the reflected light will form an image that is in the plane of Fig. 2 and perpendicular to the incident beam. This is because the sagittal focus is the center of curvature of the surface perpendicular to the Fig. 2.

If that same beam is focused at the tangential focus, the line image formed by the reflected light will be perpendicular to Fig. 2. This is because the tangential focus is the center of curvature of the surface in the plane of Fig. 2. If one were to draw a circle whose center was the tangential focus and radius was R_t, the circle would be precisely tangent to the parabola at y = 10. Fig. 4 shows the geometry of the parabola and ASM probe beams before rotating the model.

This rather simple model was used as an aid in setting up a Zemax file to analyze more general examples of probing the sagittal foci aspheric surfaces. In Zemax, it is easiest to have the light coming in through a paraxial ASM from the left impinging on the surface at normal incidence. This means rotating the surface about the sagittal focus to accomplish this. The simple parabola model made it easy to see that the Lens Data file was set up correctly for more complex cases.

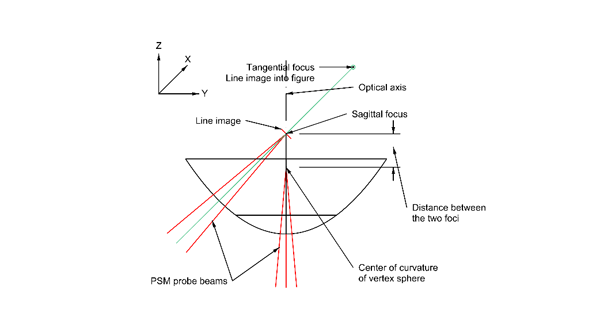
Fig. 4 Parabola model with PSM probe beams before 45 ° rotation

3.2.3 Example of investigating a general aspheric surface

Edmund Optics sells a molded plano-convex aspheric lens (P/N 69-141) of similar dimensions to the parabolic surface just used as an example. The pertinent dimensions are shown in Fig. 5 and were derived from the information that Edmund² makes available on line or via the Zemax lens files. In the case of this lens a convenient tilt to probe the sagittal focus without vignetting the beam at the edge of the clear aperture is about 52°. This gives a separation of the CoC from the sagittal focus of 3.73 mm, a number that gives the sensitivity of the determination of the optical axis.

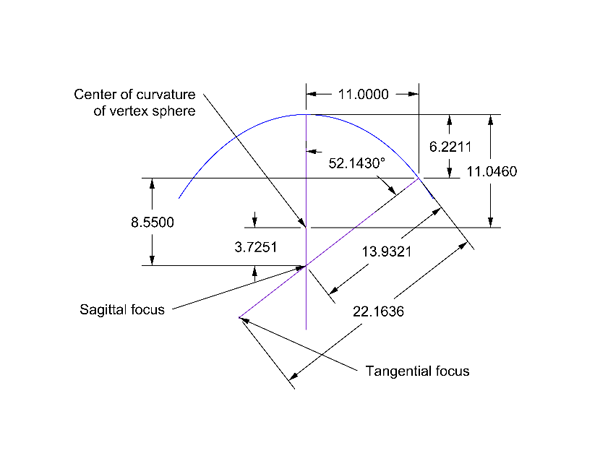
Fig. 5 Pertinent dimensions of Edmund aspheric lens 69-141 for determining the optical axis

This lens was set up on a precision, air bearing, rotary table so that it could be viewed by two PSM’s, one looking down on axis and the other looking along a normal at 52° from the axis of the table. The setup is shown in Fig. 6.

The PSM on the left that is viewing the sagittal focus does not appear to have an objective, but it does have a 50 mm efl doublet used as an objective to give sufficient working distance so the two objectives do not interfere when making simultaneous measurements.

The first measurement done was to check the centering of the CoC of the vertex sphere with the PSM looking down the axis of the asphere. Fig. 7 shows the data from this measurement where data was taken for about 2.5 complete revolutions of the rotary table. The measurement data were continuous scans of the x and y reflected image positions from the CoC versus the table rotation axis. By taking multiple rotations it gives a feel for the repeatability of the data. To begin, the lens was reasonably well centered but, as the data shows, not to the level of sensitivity of the PSM.

Fig. 6 Edmund 69-141 lens on a rotary table being viewed by two PSM’s

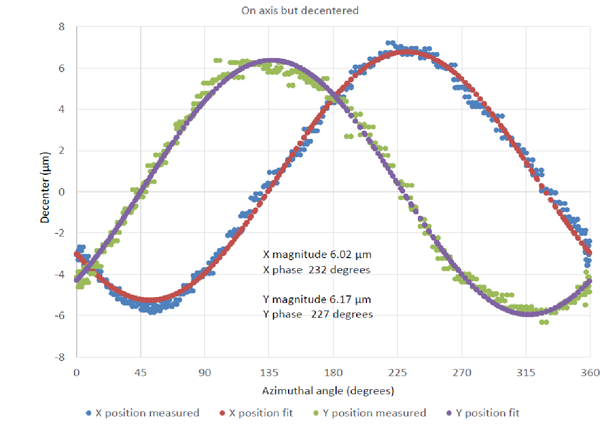
Fig. 7 Measurement of the centering of the CoC of the Edmund lens before adjusting the centering

This data set is instructive from several viewpoints. First, the repeatability revolution to revolution is at the sub-micron level. When the data were least squares fit with sin curves the magnitudes and phases should have been identical if there were no measurement error. In fact the relative error in magnitude was about 2.5% and the relative phase error about 1.4%, rather good considering a centering error of about 6 μm. Further, the data indicates the azimuthal orientation of the centering error so that it can be corrected.

Before centering the lens the error at the sagittal focus was measured and is shown in Fig. 8. Here only the x direction data is shown as explained previously because of the line image. Again the repeatability for multiple rotations is sub-micron and very sinusoidal.

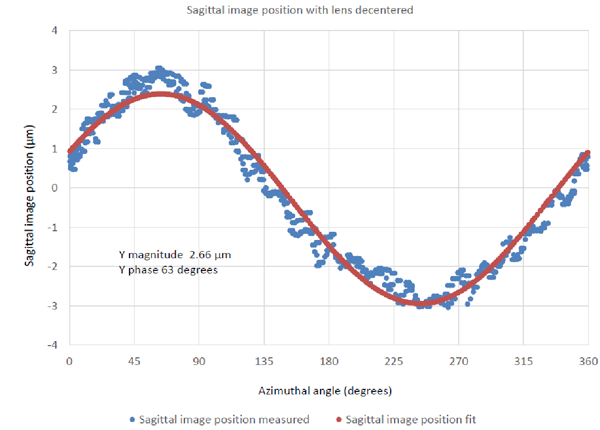
Fig. 8 Measurement of the centering error of the sagittal focus

The lens was then translated to center the CoC as well as could be done given the limits of hardware and software. Fig. 9 shows the residual centering error of the CoC which is about 0.3 μm when the x and y data are averaged and it is recalled that the graph shows the total runout, twice the actual decenter from the rotary table axis.

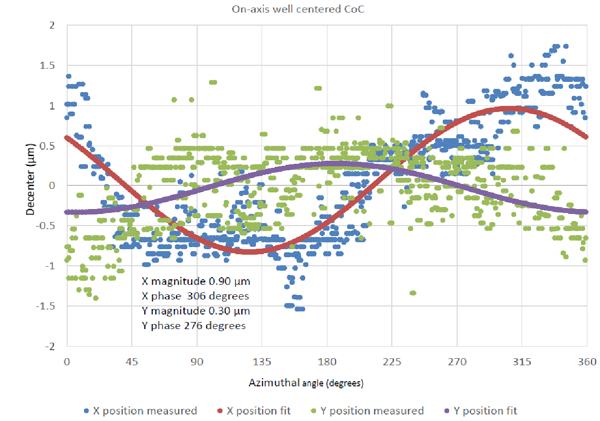
Fig. 9 Residual centering error after best attempt at centering the CoC of the vertex sphere

Following the centering of the CoC the sagittal focus was re-measured without making any further adjustments, and this result is shown in Fig. 10. The magnitude of the error is slightly greater than before centering and the phase about 84°. This means the tilt of the optical axis is about 1.3 mradians relative to the rotary table axis.

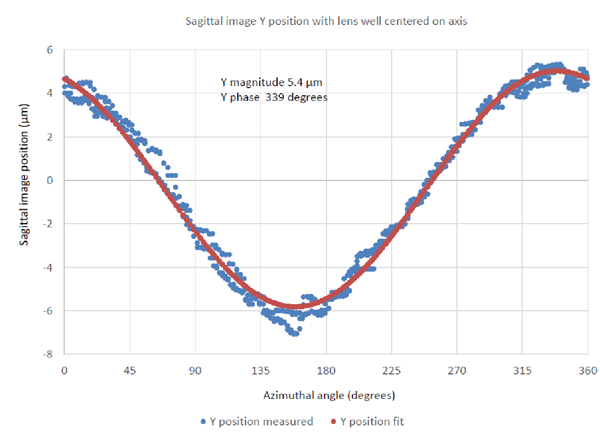
Fig. 10 Centering error in the sagittal focus after center the CoC

3.3 Centering both sides of the plano-convex lens simultaneously

Since the lens in the example has a plano backside it is also possible the determine the tilt of the plano side relative to the rotary table axis by moving the on-axis PSM to the back focus of the lens as shown in Fig. 11 where the optics of the PSM are modelled as paraxial lenses. 

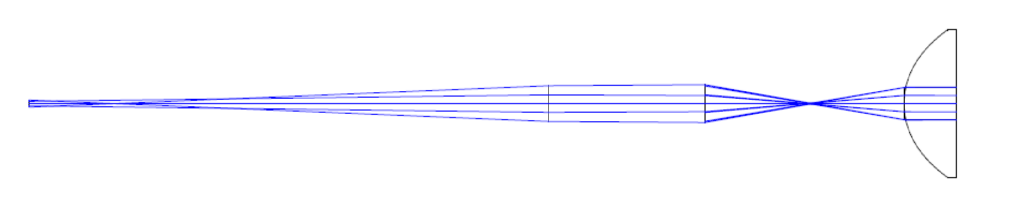
Fig. 11 Rays from the PSM on-axis at the back focus of the Edmund lens

The back focus is 18.75 mm above the lens while the objective is focused 11.046 mm below the surface to focus at the CoC for a total focus shift of about 29.80 mm. In this back focus position, Fig. 12 shows the decenter of the spot from rays reflected off the plano surface. These curves look very similar to all the previous centering data with the exception that the decenter is larger and the two curves do not appear to be centered evenly about zero decenter. The even decenter about zero simply has to do with where the center of the reference in the ASM was set at the beginning of the measurement, and has no bearing on the data other than aesthetics. The fact that the decenter magnitude is much larger has to do with the much longer baseline over which the decenter is measured.

This data was taken when the CoC was centered as best we could and the CoC is 29.80 mm from the back focus. Thus the tilt of the plano surface is 53.3 μm/2*29800 μm = 0.89 mradians at an azimuthal angle of 252.5°, close to the angle of the optical axis relative to the rotary table. It appears that this lens is quite free of tilt between the aspheric surface and the plano side. The long distance between the two foci on axis gives a high sensitivity to this measurement of wedge in the lens.

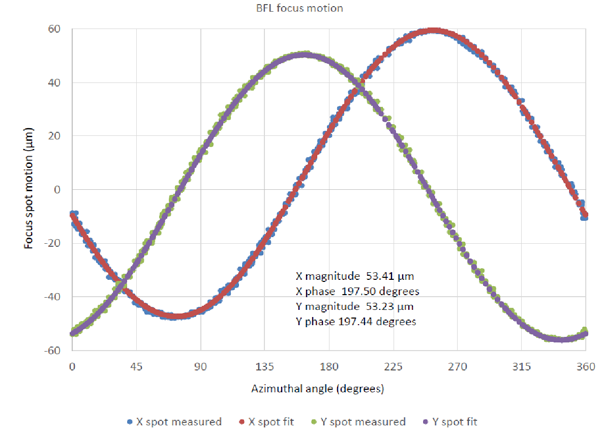
Fig. 12 Decenter of the back focus of the lens

Because it was now obvious that 3 measurements could be made on the plano-convex asphere without moving the lens from its original fixture, it was decided to see if tilting and decentering the element could bring the optical axis of the whole element in line with the axis of the rotary table. By alternately focusing first at the CoC and then the back focus it was possible to center both conjugates to less than 1 μm. Given the nearly 30 mm distance between conjugates this means the error between the optical axis and the rotary table axis were no more than about 7 arc seconds. With this degree of alignment, another measurement was made of the centering error at the sagittal focus as shown in Fig. 13.

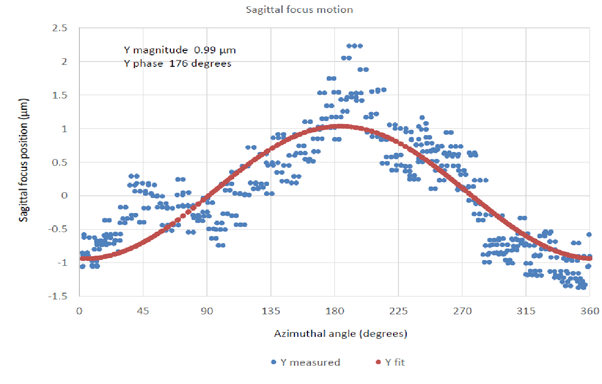
Fig. 13 Residual decenter of the sagittal focus after alignment of the back and CoC foci

This alignment of both sides of the shows the alignment can be done to high precision without having to turn the lens over to center the second side. We will go on to show that this works in the cases of both a spherical surface on the second side and an aspheric surface. By aligning both sides of a lens in one set up it eliminates the possibility of introducing mechanical misalignments in the process of turning the lens over so the second side can be measured. In this approach the only necessary condition is to align the first surface as well as possible to the axis of the rotary table so that when looking through the first surface the error in the alignment of that surface does not affect the measurements of the second side.

The only regret in this whole exercise was that it was not possible to get a mechanical indicator in the set up to measure the runout of the periphery of the lens. This would have shown whether the periphery could have been relied on to center this otherwise very good lens in terms of centering.

3.4 Measuring the alignment of two aspheric surfaces on a single lens in one setup

It is difficult to find a design of a lens with an asphere on both sides because of proprietary design issues but it is easy to illustrate using this method of alignment by going back to a lens with parabolic surfaces on both sides. The example is general and the explanation is simple because of the simple nature of the surfaces. Start with the parabolic surface shown in Fig. 1 and add to it a second positive parabolic surface with a vertex radius of 20 mm and a central thickness of 14 mm. Assume the element is 25 mm in diameter and made of a glass of index 1.6 to produce a lens the looks like Fig. 14 (a).

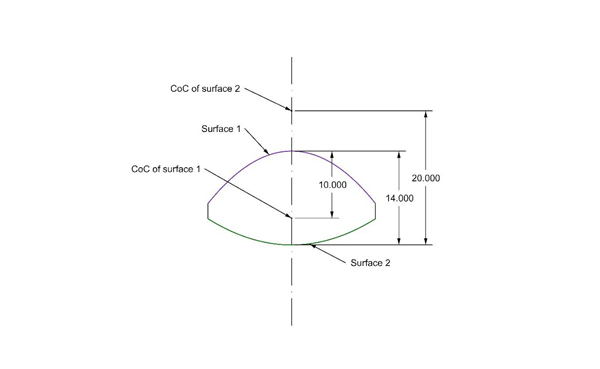
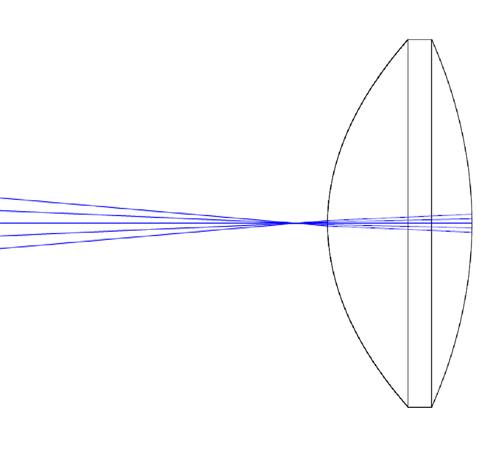
Fig. 14 (a) Double side parabolic aspheric lens (b) PSM at optical CoC of side 1

Assume the lens is sitting on a rotary table and side 1 has been centered in tilt and decenter relative to the rotary table axis as well as possible. The PSM that is on axis is used to look at the optical CoC of side 2 to determine whether that CoC is decentered. That configuration looks like Fig. 14 (b) where much of the PSM optics have been left out in order to better see the rays in the lens. If side 2 of the lens is decentered the index of the glass increases the sensitivity to decenter by the index, so a decenter of 1 μm leads to a TIR spot motion of 3.2 μ in this case of the 1.6 index. The index does not affect the apparent sensitivity to tilt because although it is affected, the greater sensitivity is reciprocally cancelled because of the apparent shorter lever arm the tilt acts over. However, by just looking on axis we cannot tell whether the motion in the reflected spot is due to decenter of the CoC or a tilt of side 2.

To check on side 2 to separate tilt from decenter there are an infinite number of solutions but introducing the PSM probe beam at an arbitrary angle as shown in Fig. 15, the light is reflected off the local CoC of a patch of the surface of side 2. Fig. 15 is complex but matches the Zemax model of this same situation exactly. The vertex of the lens was at 0,0 to begin with. It was arbitrarily decentered -3 mm and then tilted 26° about a point 3.994 mm beyond where the vertex was originally. Once this was done it is not hard to show the angle of incidence is 34.194° which makes the angle of refraction 20.563° where we use an index of 1.6. Fig. 16 (a) shows the Zemax layout of the model lens in Fig. 14 and Fig. 16 (b) shows the tangential image which is diffraction limited in the narrow direction.

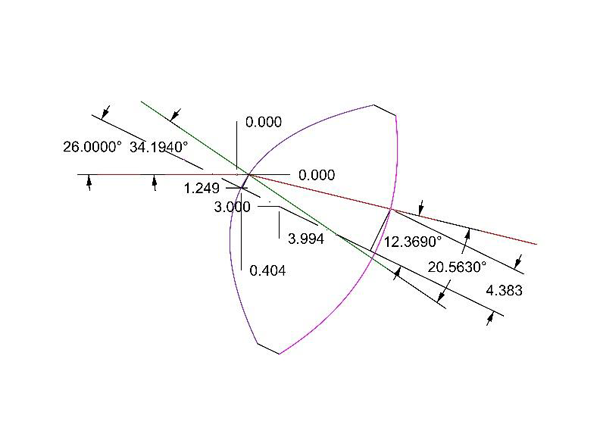
Fig. 15 Double parabolic lens tilted and decentered so incident ray reflects normally at side 2

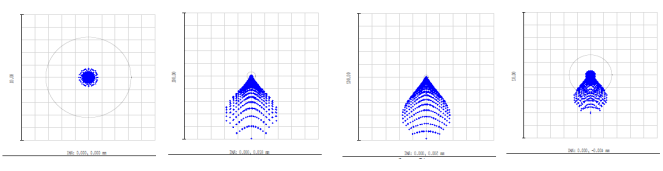
Fig. 16 (a) Zemax model showing the ray bundle reflecting off side 2 and (b) the tangential image seen in the PSM

By changing the merit function in Zemax to find the sagittal image, the thickness on surface 1 changes by 0.704 mm and the line image is vertical. The focus shift of 0.704 mm is all that is needed to go from one diffraction limited focus to the other on side 2. Either image could be used to check the centering of the second side.

It should be noted that the default Zemax merit functions that use the operands TRCX and TRCY to find Spot X or Spot Y. These operands do not work to find sagittal and tangential images. Use these default merit functions to get the pupil coordinates but change the operand from TRCX to REAX, or TRCY to REAY and enter the last surface as the place for the ray heights to be zero. This does a good job of finding the appropriate thicknesses and radii for the sagittal and tangential foci.

To conclude this aspect of the discussion it has been shown that using an ASM in two positions relative to an aspheric surface it is possible to unambiguously determine the location of the optical axis of the surface relative to the axis of a precision rotary table. Furthermore, once the first surface of the aspheric lens has been centered as well as possible to the rotary table axis, the ASM viewing the aspheric surface near its edge can be repositioned to obtain a reflection off the second surface sagittal or tangential center of curvature. Using this ASM and the ASM that is on axis but now focused at the second surface apparent center of curvature, it is possible to determine the tilt and decenter of the second aspheric surface without ever having to move the lens from its initial fixture on the rotary table. This single setup to measure the optical axis location of both surfaces leads to a more precise measurement than one where the lens must be flipped over to measure the second surface.