Chapter 23 Alignment of Convex Surfaces
This chapter may seem out of sequence, but it tackles a recurring challenge that arguably deserved attention in a previous chapter: aligning convex surfaces. These surfaces appear nearly as often as their easier-to-align concave counterparts, yet they’re frequently overlooked—perhaps because they’re more difficult to visualize and work with. But they do exist, and they can’t be ignored. So, let’s dive in.
If a convex surface has a short radius of curvature—say, less than 10 mm—it’s usually within the working distance of most microscope objectives. For instance, a common Nikon 50× objective has an 11 mm working distance, making it easy to align a 10 mm radius surface to within a fraction of a micron. Several manufacturers also offer long working distance objectives; for magnifications up to 10× (and sometimes higher), these can reach a working distance of around 35 mm. The trade-off? They’re noticeably bulkier than their short-working-distance counterparts.
If you need more than about 35 mm of working distance, a simple trick is to use a common plano-concave lens or an achromatic doublet with a focal length longer than the surface’s radius of curvature instead of a microscope objective. Since you’re using the lens on-axis and with monochromatic light, any minor aberrations will be symmetrical, and centroiding algorithms handle symmetrical images very well. The trade-off is a reduction in both lateral and axial alignment sensitivity, proportional to the ratio of the tube lens focal length to that of the objective. In many cases, though, this loss is negligible.
If you’re worried about losing sensitivity, there’s another way to extend the working distance—up to what I’d call a practical limit of 100–150 mm. Use a standard 10× objective on the PSM (or any other centering instrument) and add a 1:1 relay with an object distance in the 100-150 mm range. The catch is that you now have a lens system cantilevered out in front of the PSM, which is both vulnerable to damage if bumped and, frankly, looks a bit odd. Still, it gives you that extra working distance without sacrificing the 10× objective’s sensitivity.
Longer radii
Of course, this still doesn’t cover every practical case. The fix isn’t all that different from the 1:1 relay just discussed—you need an auxiliary lens to transform the diverging reflection from the convex surface into a converging one. To preserve sensitivity, the auxiliary lens should also be used with 1:1 conjugates. This puts a practical upper limit on the surface radius—perhaps 500 to 1000 mm—depending on the size of your optical table. For example, if you’re aligning a 1 m radius convex surface, a good choice would be a biconvex lens with an effective focal length (EFL) of 500 mm, giving you object and image distances of about 1 m each.
The first objection you’ll probably hear when suggesting this approach is something like, “But the surface we’re aligning is 100 mm in diameter—a lens that size would have to be custom-made and ridiculously expensive.” Your counter: “No need. I’ll use a 25 mm diameter catalog lens.” The pushback then becomes, “But that won’t cover the whole aperture.” This is where you explain that alignment is a first-order optical problem: if the central 25 mm of the surface is aligned to within 1 second of arc, the entire surface is aligned to that same precision. That’s because in first-order optics, small tilts or shifts measured in the central region translate directly to the same angular accuracy across the whole surface.
Once they’ve conceded that point, the next question is, “Okay, but how are you going to align this auxiliary lens?” That’s when you head to the whiteboard and sketch out the setup—see Fig. 1a. The drawing shows all the components and their final positions needed to align the convex surface (shown in green).
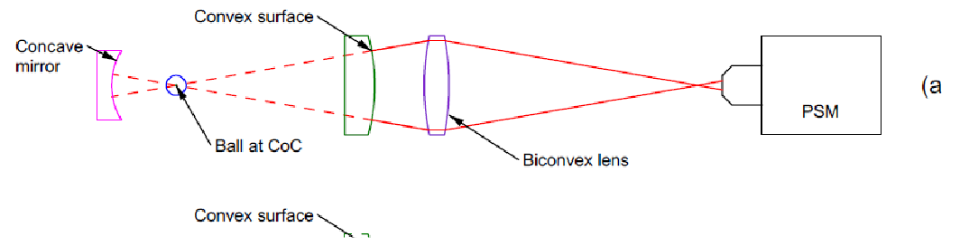
Fig. 1 Steps for aligning a convex surface using a ball reference
The first step in the alignment process—shown in Fig. 1b—is to place a specular ball so that its center sits at the intended center of curvature of the convex surface. Next (Fig. 1c), insert the biconvex lens and illuminate it using the PSM’s point source. Place a white card to the left of the biconvex lens to see where the light comes to focus. Adjust both the lens and the PSM until the object and image distances are roughly equal, and the focused spot lands on the surface of the ball. At this point, you should see a cat’s-eye reflection from the ball, centered on the PSM crosshair. Aim to center the focused spot on the ball’s surface as precisely as possible—the out-of-focus cat’s-eye will appear football-shaped unless you’re well aligned. (If you’re not well centered on the ball surface, finding the center-of-curvature reflection in the next step will be much harder.)
Next, move the PSM slightly closer to the lens, increasing the image distance so the focused spot lands at the ball’s center. You’ll see a defocused return from the ball’s center of curvature that isn’t yet on the crosshair. Make small, careful adjustments until that reflected spot is both sharply focused and centered on the crosshair. Once you’ve achieved this, the biconvex auxiliary lens is correctly positioned for aligning the convex surface—because the surface’s center of curvature now coincides with the center of the ball.
Now insert the convex surface and look for its focused reflected spot near the PSM’s outgoing focused spot. A white card placed in the path of the outgoing light makes it easier to spot the reflection. Adjust the convex mirror until the reflected spot returns into the objective and you see the image on the PSM monitor. It’s easier to start with a low-power objective to locate the spot and then switch to a higher-power objective for the final fine-tuning.
Figure 1 isn’t to scale—the proportions don’t reflect the reality of 1 m object and image distances with a 25 mm diameter biconvex auxiliary lens—but it does illustrate the principle of aligning a convex surface. An easier to initially align variation of the procedure is to replace the ball in the final step with a concave spherical mirror. At first, this might seem like a more complicated setup, but in practice it’s easier—because the mirror’s reflection is much easier to locate than the ball’s, especially as the object and image distances increase. For this version, see Figure 2.
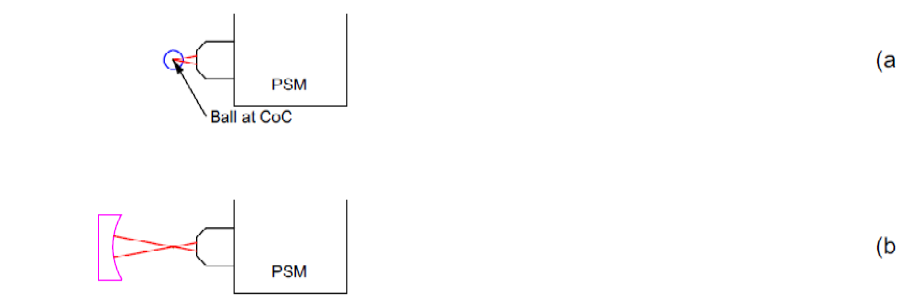
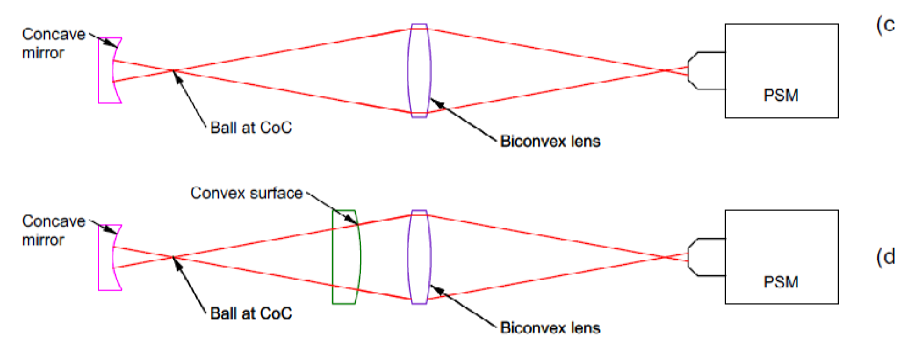
Fig. 2 Alternative method of aligning a convex surface when object and image distances are long
The procedure begins the same way as before—using a ball to define the location of the convex surface’s center of curvature. The PSM is focused on the center of the ball, making its focus coincide in all three degrees of freedom with the desired center of curvature. Then the ball is removed, and a concave spherical mirror—typically with a radius of 50 to 100 mm—is inserted and aligned so that its own center of curvature matches the PSM focus. For long object and image distances—meaning slow, low-NA light cones—it’s far easier to detect the return reflection from the concave mirror than from the short-radius ball. That’s why this approach, despite looking more elaborate, is actually easier and faster in practice.
With the concave mirror in place, insert the biconvex lens and position the PSM at its far conjugate. Using a white card, adjust the PSM so the lens forms an image of the PSM focus near the intended center of curvature of the convex surface. Use the card to help center the reflected spot from the mirror on top of the incident spot by moving the PSM. Once these spots are roughly aligned the focused image at the PSM focus should now be easy to see. Continue adjusting the PSM until the reflected spot is both centered and sharply focused on the crosshair, while keeping the lens’ object and image distances roughly equal.
Once the combination of the concave mirror, lens and PSM is finished, the convex surface is inserted just as in the case of using the ball. The convex surface is adjusted in 3 degrees of freedom until the reflection from its surface is centered on the PSM crosshair.
Although Fig. 3 may be a bit hard to interpret, it shows real hardware set up to use the ball method for aligning the convex side of a meniscus lens. An auxiliary lens was used so that the convex surface’s center of curvature lay on the center of a ball positioned midway between the meniscus and the nearer ball. The concave side of the meniscus was aligned to the ball closest to the PSM. This setup used two PSMs so that both centers of curvature could be observed at the same time—because seeing both simultaneously makes it possible to align the meniscus in both tilt and decenter in a single process.

Fig. 3 Alignment of a meniscus lens using an auxiliary lens to view the convex surface
Very long radii
When the radius of the convex surface exceeds about 1 m, it’s time to switch methods entirely. Over the PSM’s 8 mm aperture (with the objective removed so it can function as an autocollimator) a 1 m radius surface has a sag of y2/2R = 16/2000 = 8 µm, giving the surface an effective object distance of about 500 mm. With the PSM’s 100 mm EFL tube lens, this causes the image to form at 125 mm instead of at 100 mm for a collimated wavefront. The result is a 2 mm diameter image at the camera. Because the image is rotationally symmetric, the centroiding algorithm doesn’t care about its size, it simply finds the center of the intensity pattern. In fact, it can do so even more precisely, because now there are roughly 264,000 pixels to centroid on instead of just 10–20 for a sharply focused spot from a plane wavefront. For convex surfaces with radii of 1 m or more, it’s best to use the PSM as an autocollimator and centroid on this out-of-focus image.
Conclusions
There are at least two key take-aways from this discussion of convex surface alignment. First, there’s no “one-size-fits-all” approach to optical testing—you must look at the first-order geometry of your setup to decide what’s both practical and sensitive enough to get the job done. Second, while you can center a convex optic accurately over a wide range of radii if you choose the right method, judging axial distances or best focus becomes tricky when working with small-diameter optics and long radii. The problem is that the numerical aperture of the light cone is too small, and the depth of focus is proportional to the square of the NA. In the next chapter, we’ll explore ways to tackle this challenge and improve focus detection for long-radius surfaces with low-NA light cones.